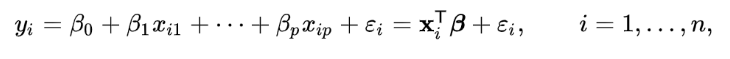Ordinary Least Squares (OLS) 

In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. 

Linear Regression 

 A linear regression model assumes that the relationship between the dependent variable y and the vector of regressors x is linear. This relationship is modeled through a disturbance term or error variable ε — an unobserved random variable that adds “noise” to the linear relationship between the dependent variable and regressors. Thus, the model takes the form: